矩阵相乘

矩阵相乘

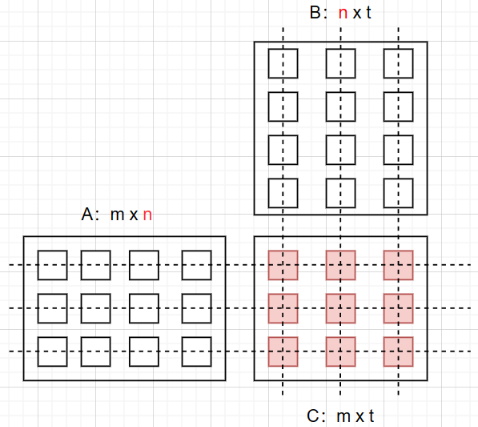
矩阵相乘：确保第一个矩阵（A矩阵）的列数等于第二个矩阵（B矩阵）的行数。如果A矩阵的大小是m × n，B矩阵的大小是n × t，那么它们可以相乘，得到的矩阵C的大小将是m × t。矩阵C中的每个元素是矩阵A对应行的元素与矩阵B对应列的元素的乘积之和。

image-20231014113746942

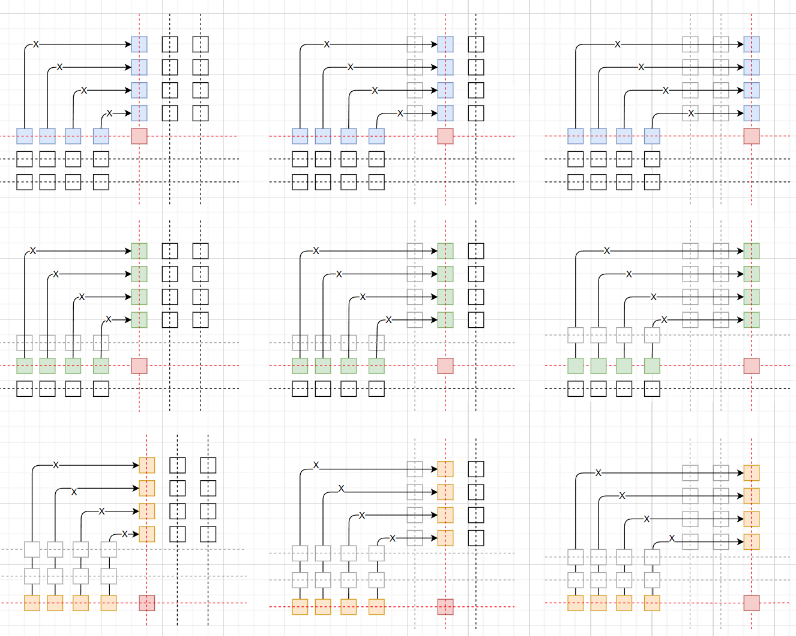
具体计算过程可以看以下图

image-20231014120013002

代码实现

c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <stdio.h>

int main()
{
    int A[3][2] = {{1, 2},
                   {3, 4},
                   {5, 6}};
    int B[2][4] = {{7, 8, 9, 10},
                   {11, 12, 13, 14}};
    int m = 3;         // C矩阵的行
    int t = 4;         // C矩阵的列
    int C[3][4] = {0}; // 注意：定义数组时，大小不可为变量，只可为常量
    // 矩阵相乘
    int i, j, k;
    for (i = 0; i < m; i++)
    {
        for (j = 0; j < t; j++)
        {
            for (k = 0; k < 2; k++) // k用来遍历矩阵A的列和矩阵B的行
            {
                C[i][j] = C[i][j] + A[i][k] * B[j][k];
            }
        }
    }

    for (i = 0; i < m; i++)
    {
        for (j = 0; j < t; j++)
        {
            printf("%d\t", C[i][j]);
        }
        printf("\n");
    }

    return 0;
}